{
"cells": [
{
"cell_type": "markdown",
"id": "21a20d87",
"metadata": {},
"source": [
"\n",
"<a id='arellano'></a>"
]
},
{
"cell_type": "markdown",
"id": "a8fda2ae",
"metadata": {},
"source": [
"# Default Risk and Income Fluctuations\n",
"\n",
"In addition to what’s in Anaconda, this lecture will need the following libraries:"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "4d932f85",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"!pip install --upgrade quantecon"
]
},
{
"cell_type": "markdown",
"id": "e568ab7a",
"metadata": {},
"source": [
"## Overview\n",
"\n",
"This lecture computes versions of Arellano’s [[Arellano, 2008](https://python-advanced.quantecon.org/zreferences.html#id129)]\n",
"model of sovereign default.\n",
"\n",
"The model describes interactions among default risk, output, and an\n",
"equilibrium interest rate that includes a premium for endogenous default risk.\n",
"\n",
"The decision maker is a government of a small open economy that borrows from\n",
"risk-neutral foreign creditors.\n",
"\n",
"The foreign lenders must be compensated for default risk.\n",
"\n",
"The government borrows and lends abroad in order to smooth the consumption of\n",
"its citizens.\n",
"\n",
"The government repays its debt only if it wants to, but declining to pay has\n",
"adverse consequences.\n",
"\n",
"The interest rate on government debt adjusts in response to the\n",
"state-dependent default probability chosen by government.\n",
"\n",
"The model yields outcomes that help interpret sovereign default experiences,\n",
"including\n",
"\n",
"- countercyclical interest rates on sovereign debt \n",
"- countercyclical trade balances \n",
"- high volatility of consumption relative to output \n",
"\n",
"\n",
"Notably, long recessions caused by bad draws in the income process increase the government’s\n",
"incentive to default.\n",
"\n",
"This can lead to\n",
"\n",
"- spikes in interest rates \n",
"- temporary losses of access to international credit markets \n",
"- large drops in output, consumption, and welfare \n",
"- large capital outflows during recessions \n",
"\n",
"\n",
"Such dynamics are consistent with experiences of many countries.\n",
"\n",
"Let’s start with some imports:"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "b0220f0a",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"import quantecon as qe\n",
"from numba import njit, prange"
]
},
{
"cell_type": "markdown",
"id": "96206643",
"metadata": {},
"source": [
"## Structure\n",
"\n",
"In this section we describe the main features of the model."
]
},
{
"cell_type": "markdown",
"id": "b21be32c",
"metadata": {},
"source": [
"### Output, Consumption and Debt\n",
"\n",
"A small open economy is endowed with an exogenous stochastically fluctuating potential output\n",
"stream $ \\{y_t\\} $.\n",
"\n",
"Potential output is realized only in periods in which the government honors its sovereign debt.\n",
"\n",
"The output good can be traded or consumed.\n",
"\n",
"The sequence $ \\{y_t\\} $ is described by a Markov process with stochastic density kernel\n",
"$ p(y, y') $.\n",
"\n",
"Households within the country are identical and rank stochastic consumption streams according to\n",
"\n",
"\n",
"<a id='equation-utility'></a>\n",
"$$\n",
"\\mathbb E \\sum_{t=0}^{\\infty} \\beta^t u(c_t) \\tag{13.1}\n",
"$$\n",
"\n",
"Here\n",
"\n",
"- $ 0 < \\beta < 1 $ is a time discount factor \n",
"- $ u $ is an increasing and strictly concave utility function \n",
"\n",
"\n",
"Consumption sequences enjoyed by households are affected by the government’s decision to borrow or\n",
"lend internationally.\n",
"\n",
"The government is benevolent in the sense that its aim is to maximize [(13.1)](#equation-utility).\n",
"\n",
"The government is the only domestic actor with access to foreign credit.\n",
"\n",
"Because household are averse to consumption fluctuations, the government will try to smooth\n",
"consumption by borrowing from (and lending to) foreign creditors."
]
},
{
"cell_type": "markdown",
"id": "27721d1d",
"metadata": {},
"source": [
"### Asset Markets\n",
"\n",
"The only credit instrument available to the government is a one-period bond traded in international credit markets.\n",
"\n",
"The bond market has the following features\n",
"\n",
"- The bond matures in one period and is not state contingent. \n",
"- A purchase of a bond with face value $ B' $ is a claim to $ B' $ units of the\n",
" consumption good next period. \n",
"- To purchase $ B' $ next period costs $ q B' $ now, or, what is equivalent. \n",
"- For selling $ -B' $ units of next period goods the seller earns $ - q B' $ of today’s\n",
" goods. \n",
" - If $ B' < 0 $, then $ -q B' $ units of the good are received in the current period,\n",
" for a promise to repay $ -B' $ units next period. \n",
" - There is an equilibrium price function $ q(B', y) $ that makes $ q $ depend on both\n",
" $ B' $ and $ y $. \n",
"\n",
"\n",
"Earnings on the government portfolio are distributed (or, if negative, taxed) lump sum to\n",
"households.\n",
"\n",
"When the government is not excluded from financial markets, the one-period national budget\n",
"constraint is\n",
"\n",
"\n",
"<a id='equation-resource'></a>\n",
"$$\n",
"c = y + B - q(B', y) B' \\tag{13.2}\n",
"$$\n",
"\n",
"Here and below, a prime denotes a next period value or a claim maturing next period.\n",
"\n",
"To rule out Ponzi schemes, we also require that $ B \\geq -Z $ in every period.\n",
"\n",
"- $ Z $ is chosen to be sufficiently large that the constraint never binds in equilibrium. "
]
},
{
"cell_type": "markdown",
"id": "5b93d28f",
"metadata": {},
"source": [
"### Financial Markets\n",
"\n",
"Foreign creditors\n",
"\n",
"- are risk neutral \n",
"- know the domestic output stochastic process $ \\{y_t\\} $ and observe\n",
" $ y_t, y_{t-1}, \\ldots, $ at time $ t $ \n",
"- can borrow or lend without limit in an international credit market at a constant international\n",
" interest rate $ r $ \n",
"- receive full payment if the government chooses to pay \n",
"- receive zero if the government defaults on its one-period debt due \n",
"\n",
"\n",
"When a government is expected to default next period with probability $ \\delta $, the expected\n",
"value of a promise to pay one unit of consumption next period is $ 1 - \\delta $.\n",
"\n",
"Therefore, the discounted expected value of a promise to pay $ B $ next period is\n",
"\n",
"\n",
"<a id='equation-epc'></a>\n",
"$$\n",
"q = \\frac{1 - \\delta}{1 + r} \\tag{13.3}\n",
"$$\n",
"\n",
"Next we turn to how the government in effect chooses the default probability $ \\delta $."
]
},
{
"cell_type": "markdown",
"id": "77030375",
"metadata": {},
"source": [
"### Government’s Decisions\n",
"\n",
"At each point in time $ t $, the government chooses between\n",
"\n",
"1. defaulting \n",
"1. meeting its current obligations and purchasing or selling an optimal quantity of one-period\n",
" sovereign debt \n",
"\n",
"\n",
"Defaulting means declining to repay all of its current obligations.\n",
"\n",
"If the government defaults in the current period, then consumption equals current output.\n",
"\n",
"But a sovereign default has two consequences:\n",
"\n",
"1. Output immediately falls from $ y $ to $ h(y) $, where $ 0 \\leq h(y) \\leq y $. \n",
" - It returns to $ y $ only after the country regains access to international credit\n",
" markets. \n",
"1. The country loses access to foreign credit markets. "
]
},
{
"cell_type": "markdown",
"id": "d4a7003a",
"metadata": {},
"source": [
"### Reentering International Credit Market\n",
"\n",
"While in a state of default, the economy regains access to foreign credit in each subsequent\n",
"period with probability $ \\theta $."
]
},
{
"cell_type": "markdown",
"id": "0c9ac1d2",
"metadata": {},
"source": [
"## Equilibrium\n",
"\n",
"Informally, an equilibrium is a sequence of interest rates on its sovereign debt, a stochastic\n",
"sequence of government default decisions and an implied flow of household consumption such that\n",
"\n",
"1. Consumption and assets satisfy the national budget constraint. \n",
"1. The government maximizes household utility taking into account \n",
" - the resource constraint \n",
" - the effect of its choices on the price of bonds \n",
" - consequences of defaulting now for future net output and future borrowing and lending\n",
" opportunities \n",
"1. The interest rate on the government’s debt includes a risk-premium sufficient to make foreign\n",
" creditors expect on average to earn the constant risk-free international interest rate. \n",
"\n",
"\n",
"To express these ideas more precisely, consider first the choices of the government, which\n",
"\n",
"1. enters a period with initial assets $ B $, or what is the same thing, initial debt to be\n",
" repaid now of $ -B $ \n",
"1. observes current output $ y $, and \n",
"1. chooses either \n",
" 1. to default, or \n",
" 1. to pay $ -B $ and set next period’s debt due to $ -B' $ \n",
"\n",
"\n",
"In a recursive formulation,\n",
"\n",
"- state variables for the government comprise the pair $ (B, y) $ \n",
"- $ v(B, y) $ is the optimum value of the government’s problem when at the beginning of a\n",
" period it faces the choice of whether to honor or default \n",
"- $ v_c(B, y) $ is the value of choosing to pay obligations falling due \n",
"- $ v_d(y) $ is the value of choosing to default \n",
"\n",
"\n",
"$ v_d(y) $ does not depend on $ B $ because, when access to credit is eventually regained,\n",
"net foreign assets equal $ 0 $.\n",
"\n",
"Expressed recursively, the value of defaulting is\n",
"\n",
"$$\n",
"v_d(y) = u(h(y)) +\n",
" \\beta \\int \\left\\{\n",
" \\theta v(0, y') + (1 - \\theta) v_d(y')\n",
" \\right\\}\n",
" p(y, y') dy'\n",
"$$\n",
"\n",
"The value of paying is\n",
"\n",
"$$\n",
"v_c(B, y) = \\max_{B' \\geq -Z}\n",
" \\left\\{\n",
" u(y - q(B', y) B' + B) +\n",
" \\beta \\int v(B', y') p(y, y') dy'\n",
" \\right\\}\n",
"$$\n",
"\n",
"The three value functions are linked by\n",
"\n",
"$$\n",
"v(B, y) = \\max\\{ v_c(B, y), v_d(y) \\}\n",
"$$\n",
"\n",
"The government chooses to default when\n",
"\n",
"$$\n",
"v_c(B, y) < v_d(y)\n",
"$$\n",
"\n",
"and hence given $ B' $ the probability of default next period is\n",
"\n",
"\n",
"<a id='equation-delta'></a>\n",
"$$\n",
"\\delta(B', y) := \\int \\mathbb 1\\{v_c(B', y') < v_d(y') \\} p(y, y') dy' \\tag{13.4}\n",
"$$\n",
"\n",
"Given zero profits for foreign creditors in equilibrium, we can combine [(13.3)](#equation-epc) and [(13.4)](#equation-delta)\n",
"to pin down the bond price function:\n",
"\n",
"\n",
"<a id='equation-bondprice'></a>\n",
"$$\n",
"q(B', y) = \\frac{1 - \\delta(B', y)}{1 + r} \\tag{13.5}\n",
"$$"
]
},
{
"cell_type": "markdown",
"id": "403c5fa1",
"metadata": {},
"source": [
"### Definition of Equilibrium\n",
"\n",
"An *equilibrium* is\n",
"\n",
"- a pricing function $ q(B',y) $, \n",
"- a triple of value functions $ (v_c(B, y), v_d(y), v(B,y)) $, \n",
"- a decision rule telling the government when to default and when to pay as a function of the state\n",
" $ (B, y) $, and \n",
"- an asset accumulation rule that, conditional on choosing not to default, maps $ (B,y) $ into\n",
" $ B' $ \n",
"\n",
"\n",
"such that\n",
"\n",
"- The three Bellman equations for $ (v_c(B, y), v_d(y), v(B,y)) $ are satisfied \n",
"- Given the price function $ q(B',y) $, the default decision rule and the asset accumulation\n",
" decision rule attain the optimal value function $ v(B,y) $, and \n",
"- The price function $ q(B',y) $ satisfies equation [(13.5)](#equation-bondprice) "
]
},
{
"cell_type": "markdown",
"id": "889a5db2",
"metadata": {},
"source": [
"## Computation\n",
"\n",
"Let’s now compute an equilibrium of Arellano’s model.\n",
"\n",
"The equilibrium objects are the value function $ v(B, y) $, the associated\n",
"default decision rule, and the pricing function $ q(B', y) $.\n",
"\n",
"We’ll use our code to replicate Arellano’s results.\n",
"\n",
"After that we’ll perform some additional simulations.\n",
"\n",
"We use a slightly modified version of the algorithm recommended by Arellano.\n",
"\n",
"- The appendix to [[Arellano, 2008](https://python-advanced.quantecon.org/zreferences.html#id129)] recommends value function iteration until\n",
" convergence, updating the price, and then repeating. \n",
"- Instead, we update the bond price at every value function iteration step. \n",
"\n",
"\n",
"The second approach is faster and the two different procedures deliver very similar results.\n",
"\n",
"Here is a more detailed description of our algorithm:\n",
"\n",
"1. Guess a pair of non-default and default value functions $ v_c $ and $ v_d $. \n",
"1. Using these functions, calculate the value function $ v $, the corresponding default probabilities and the price function $ q $. \n",
"1. At each pair $ (B, y) $, \n",
" 1. update the value of defaulting $ v_d(y) $. \n",
" 1. update the value of remaining $ v_c(B, y) $. \n",
"1. Check for convergence. If converged, stop – if not, go to step 2. \n",
"\n",
"\n",
"We use simple discretization on a grid of asset holdings and income levels.\n",
"\n",
"The output process is discretized using a [quadrature method due to Tauchen](https://github.com/QuantEcon/QuantEcon.py/blob/master/quantecon/markov/approximation.py).\n",
"\n",
"As we have in other places, we accelerate our code using Numba.\n",
"\n",
"We define a class that will store parameters, grids and transition\n",
"probabilities."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "5c19de67",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"class Arellano_Economy:\n",
" \" Stores data and creates primitives for the Arellano economy. \"\n",
"\n",
" def __init__(self,\n",
" B_grid_size= 251, # Grid size for bonds\n",
" B_grid_min=-0.45, # Smallest B value\n",
" B_grid_max=0.45, # Largest B value\n",
" y_grid_size=51, # Grid size for income\n",
" β=0.953, # Time discount parameter\n",
" γ=2.0, # Utility parameter\n",
" r=0.017, # Lending rate\n",
" ρ=0.945, # Persistence in the income process\n",
" η=0.025, # Standard deviation of the income process\n",
" θ=0.282, # Prob of re-entering financial markets\n",
" def_y_param=0.969): # Parameter governing income in default\n",
"\n",
" # Save parameters\n",
" self.β, self.γ, self.r, = β, γ, r\n",
" self.ρ, self.η, self.θ = ρ, η, θ\n",
"\n",
" self.y_grid_size = y_grid_size\n",
" self.B_grid_size = B_grid_size\n",
" self.B_grid = np.linspace(B_grid_min, B_grid_max, B_grid_size)\n",
" mc = qe.markov.tauchen(y_grid_size, ρ, η, 0, 3)\n",
" self.y_grid, self.P = np.exp(mc.state_values), mc.P\n",
"\n",
" # The index at which B_grid is (close to) zero\n",
" self.B0_idx = np.searchsorted(self.B_grid, 1e-10)\n",
"\n",
" # Output recieved while in default, with same shape as y_grid\n",
" self.def_y = np.minimum(def_y_param * np.mean(self.y_grid), self.y_grid)\n",
"\n",
" def params(self):\n",
" return self.β, self.γ, self.r, self.ρ, self.η, self.θ\n",
"\n",
" def arrays(self):\n",
" return self.P, self.y_grid, self.B_grid, self.def_y, self.B0_idx"
]
},
{
"cell_type": "markdown",
"id": "70dcffbe",
"metadata": {},
"source": [
"Notice how the class returns the data it stores as simple numerical values and\n",
"arrays via the methods `params` and `arrays`.\n",
"\n",
"We will use this data in the Numba-jitted functions defined below.\n",
"\n",
"Jitted functions prefer simple arguments, since type inference is easier.\n",
"\n",
"Here is the utility function."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "693f7f06",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"@njit\n",
"def u(c, γ):\n",
" return c**(1-γ)/(1-γ)"
]
},
{
"cell_type": "markdown",
"id": "e1b865c7",
"metadata": {},
"source": [
"Here is a function to compute the bond price at each state, given $ v_c $ and\n",
"$ v_d $."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "96e7c35a",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"@njit\n",
"def compute_q(v_c, v_d, q, params, arrays):\n",
" \"\"\"\n",
" Compute the bond price function q(b, y) at each (b, y) pair.\n",
"\n",
" This function writes to the array q that is passed in as an argument.\n",
" \"\"\"\n",
"\n",
" # Unpack\n",
" β, γ, r, ρ, η, θ = params\n",
" P, y_grid, B_grid, def_y, B0_idx = arrays\n",
"\n",
" for B_idx in range(len(B_grid)):\n",
" for y_idx in range(len(y_grid)):\n",
" # Compute default probability and corresponding bond price\n",
" delta = P[y_idx, v_c[B_idx, :] < v_d].sum()\n",
" q[B_idx, y_idx] = (1 - delta ) / (1 + r)"
]
},
{
"cell_type": "markdown",
"id": "dcff5d24",
"metadata": {},
"source": [
"Next we introduce Bellman operators that updated $ v_d $ and $ v_c $."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "7d2b5eb5",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"@njit\n",
"def T_d(y_idx, v_c, v_d, params, arrays):\n",
" \"\"\"\n",
" The RHS of the Bellman equation when income is at index y_idx and\n",
" the country has chosen to default. Returns an update of v_d.\n",
" \"\"\"\n",
" # Unpack\n",
" β, γ, r, ρ, η, θ = params\n",
" P, y_grid, B_grid, def_y, B0_idx = arrays\n",
"\n",
" current_utility = u(def_y[y_idx], γ)\n",
" v = np.maximum(v_c[B0_idx, :], v_d)\n",
" cont_value = np.sum((θ * v + (1 - θ) * v_d) * P[y_idx, :])\n",
"\n",
" return current_utility + β * cont_value\n",
"\n",
"\n",
"@njit\n",
"def T_c(B_idx, y_idx, v_c, v_d, q, params, arrays):\n",
" \"\"\"\n",
" The RHS of the Bellman equation when the country is not in a\n",
" defaulted state on their debt. Returns a value that corresponds to\n",
" v_c[B_idx, y_idx], as well as the optimal level of bond sales B'.\n",
" \"\"\"\n",
" # Unpack\n",
" β, γ, r, ρ, η, θ = params\n",
" P, y_grid, B_grid, def_y, B0_idx = arrays\n",
" B = B_grid[B_idx]\n",
" y = y_grid[y_idx]\n",
"\n",
" # Compute the RHS of Bellman equation\n",
" current_max = -1e10\n",
" # Step through choices of next period B'\n",
" for Bp_idx, Bp in enumerate(B_grid):\n",
" c = y + B - q[Bp_idx, y_idx] * Bp\n",
" if c > 0:\n",
" v = np.maximum(v_c[Bp_idx, :], v_d)\n",
" val = u(c, γ) + β * np.sum(v * P[y_idx, :])\n",
" if val > current_max:\n",
" current_max = val\n",
" Bp_star_idx = Bp_idx\n",
" return current_max, Bp_star_idx"
]
},
{
"cell_type": "markdown",
"id": "2f5d9171",
"metadata": {},
"source": [
"Here is a fast function that calls these operators in the right sequence."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "c1faf835",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"@njit(parallel=True)\n",
"def update_values_and_prices(v_c, v_d, # Current guess of value functions\n",
" B_star, q, # Arrays to be written to\n",
" params, arrays):\n",
"\n",
" # Unpack\n",
" β, γ, r, ρ, η, θ = params\n",
" P, y_grid, B_grid, def_y, B0_idx = arrays\n",
" y_grid_size = len(y_grid)\n",
" B_grid_size = len(B_grid)\n",
"\n",
" # Compute bond prices and write them to q\n",
" compute_q(v_c, v_d, q, params, arrays)\n",
"\n",
" # Allocate memory\n",
" new_v_c = np.empty_like(v_c)\n",
" new_v_d = np.empty_like(v_d)\n",
"\n",
" # Calculate and return new guesses for v_c and v_d\n",
" for y_idx in prange(y_grid_size):\n",
" new_v_d[y_idx] = T_d(y_idx, v_c, v_d, params, arrays)\n",
" for B_idx in range(B_grid_size):\n",
" new_v_c[B_idx, y_idx], Bp_idx = T_c(B_idx, y_idx,\n",
" v_c, v_d, q, params, arrays)\n",
" B_star[B_idx, y_idx] = Bp_idx\n",
"\n",
" return new_v_c, new_v_d"
]
},
{
"cell_type": "markdown",
"id": "b0dfdf23",
"metadata": {},
"source": [
"We can now write a function that will use the `Arellano_Economy` class and the\n",
"functions defined above to compute the solution to our model.\n",
"\n",
"We do not need to JIT compile this function since it only consists of outer\n",
"loops (and JIT compiling makes almost zero difference).\n",
"\n",
"In fact, one of the jobs of this function is to take an instance of\n",
"`Arellano_Economy`, which is hard for the JIT compiler to handle, and strip it\n",
"down to more basic objects, which are then passed out to jitted functions."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "1821c48b",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"def solve(model, tol=1e-8, max_iter=10_000):\n",
" \"\"\"\n",
" Given an instance of Arellano_Economy, this function computes the optimal\n",
" policy and value functions.\n",
" \"\"\"\n",
" # Unpack\n",
" params = model.params()\n",
" arrays = model.arrays()\n",
" y_grid_size, B_grid_size = model.y_grid_size, model.B_grid_size\n",
"\n",
" # Initial conditions for v_c and v_d\n",
" v_c = np.zeros((B_grid_size, y_grid_size))\n",
" v_d = np.zeros(y_grid_size)\n",
"\n",
" # Allocate memory\n",
" q = np.empty_like(v_c)\n",
" B_star = np.empty_like(v_c, dtype=int)\n",
"\n",
" current_iter = 0\n",
" dist = np.inf\n",
" while (current_iter < max_iter) and (dist > tol):\n",
"\n",
" if current_iter % 100 == 0:\n",
" print(f\"Entering iteration {current_iter}.\")\n",
"\n",
" new_v_c, new_v_d = update_values_and_prices(v_c, v_d, B_star, q, params, arrays)\n",
" # Check tolerance and update\n",
" dist = np.max(np.abs(new_v_c - v_c)) + np.max(np.abs(new_v_d - v_d))\n",
" v_c = new_v_c\n",
" v_d = new_v_d\n",
" current_iter += 1\n",
"\n",
" print(f\"Terminating at iteration {current_iter}.\")\n",
" return v_c, v_d, q, B_star"
]
},
{
"cell_type": "markdown",
"id": "26dac779",
"metadata": {},
"source": [
"Finally, we write a function that will allow us to simulate the economy once\n",
"we have the policy functions"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "9de153ab",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"def simulate(model, T, v_c, v_d, q, B_star, y_idx=None, B_idx=None):\n",
" \"\"\"\n",
" Simulates the Arellano 2008 model of sovereign debt\n",
"\n",
" Here `model` is an instance of `Arellano_Economy` and `T` is the length of\n",
" the simulation. Endogenous objects `v_c`, `v_d`, `q` and `B_star` are\n",
" assumed to come from a solution to `model`.\n",
"\n",
" \"\"\"\n",
" # Unpack elements of the model\n",
" B0_idx = model.B0_idx\n",
" y_grid = model.y_grid\n",
" B_grid, y_grid, P = model.B_grid, model.y_grid, model.P\n",
"\n",
" # Set initial conditions to middle of grids\n",
" if y_idx == None:\n",
" y_idx = np.searchsorted(y_grid, y_grid.mean())\n",
" if B_idx == None:\n",
" B_idx = B0_idx\n",
" in_default = False\n",
"\n",
" # Create Markov chain and simulate income process\n",
" mc = qe.MarkovChain(P, y_grid)\n",
" y_sim_indices = mc.simulate_indices(T+1, init=y_idx)\n",
"\n",
" # Allocate memory for outputs\n",
" y_sim = np.empty(T)\n",
" y_a_sim = np.empty(T)\n",
" B_sim = np.empty(T)\n",
" q_sim = np.empty(T)\n",
" d_sim = np.empty(T, dtype=int)\n",
"\n",
" # Perform simulation\n",
" t = 0\n",
" while t < T:\n",
"\n",
" # Store the value of y_t and B_t\n",
" y_sim[t] = y_grid[y_idx]\n",
" B_sim[t] = B_grid[B_idx]\n",
"\n",
" # if in default:\n",
" if v_c[B_idx, y_idx] < v_d[y_idx] or in_default:\n",
" y_a_sim[t] = model.def_y[y_idx]\n",
" d_sim[t] = 1\n",
" Bp_idx = B0_idx\n",
" # Re-enter financial markets next period with prob θ\n",
" in_default = False if np.random.rand() < model.θ else True\n",
" else:\n",
" y_a_sim[t] = y_sim[t]\n",
" d_sim[t] = 0\n",
" Bp_idx = B_star[B_idx, y_idx]\n",
"\n",
" q_sim[t] = q[Bp_idx, y_idx]\n",
"\n",
" # Update time and indices\n",
" t += 1\n",
" y_idx = y_sim_indices[t]\n",
" B_idx = Bp_idx\n",
"\n",
" return y_sim, y_a_sim, B_sim, q_sim, d_sim"
]
},
{
"cell_type": "markdown",
"id": "52cc6fea",
"metadata": {},
"source": [
"## Results\n",
"\n",
"Let’s start by trying to replicate the results obtained in\n",
"[[Arellano, 2008](https://python-advanced.quantecon.org/zreferences.html#id129)].\n",
"\n",
"In what follows, all results are computed using Arellano’s parameter values.\n",
"\n",
"The values can be seen in the `__init__` method of the `Arellano_Economy`\n",
"shown above.\n",
"\n",
"For example, `r=0.017` matches the average quarterly rate on a 5 year US treasury over the period 1983–2001.\n",
"\n",
"Details on how to compute the figures are reported as solutions to the\n",
"exercises.\n",
"\n",
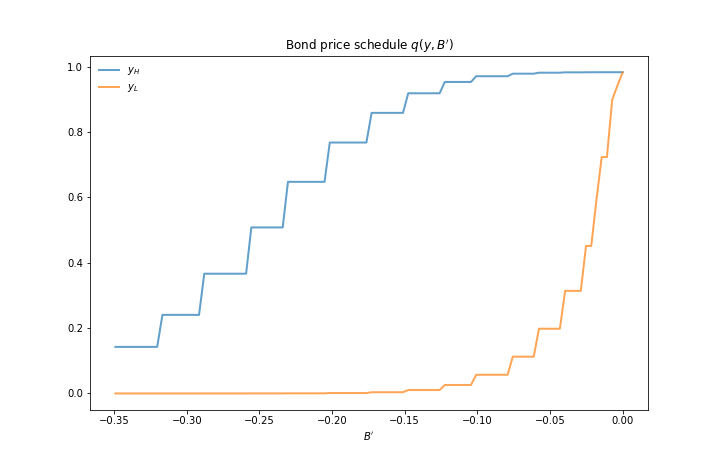
"The first figure shows the bond price schedule and replicates Figure 3 of\n",
"Arellano, where $ y_L $ and $ Y_H $ are particular below average and above average\n",
"values of output $ y $.\n",
"\n",
"\n",
"\n",
" \n",
"- $ y_L $ is 5% below the mean of the $ y $ grid values \n",
"- $ y_H $ is 5% above the mean of the $ y $ grid values \n",
"\n",
"\n",
"The grid used to compute this figure was relatively fine (`y_grid_size, B_grid_size = 51, 251`), which explains the minor differences between this and\n",
"Arrelano’s figure.\n",
"\n",
"The figure shows that\n",
"\n",
"- Higher levels of debt (larger $ -B' $) induce larger discounts on the face value, which\n",
" correspond to higher interest rates. \n",
"- Lower income also causes more discounting, as foreign creditors anticipate greater likelihood\n",
" of default. \n",
"\n",
"\n",
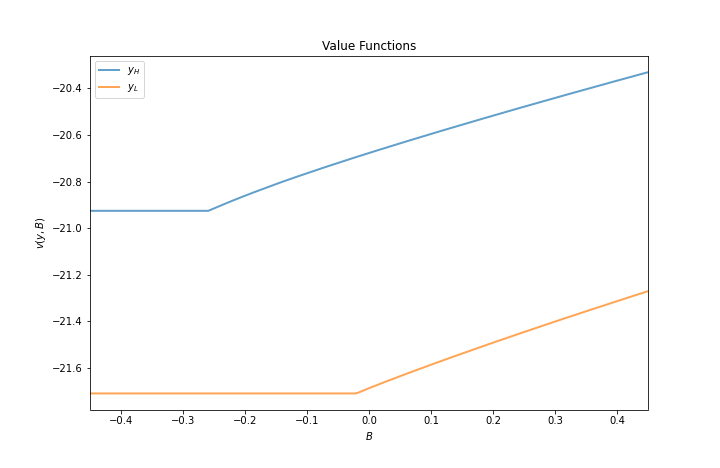
"The next figure plots value functions and replicates the right hand panel of Figure 4 of\n",
"[[Arellano, 2008](https://python-advanced.quantecon.org/zreferences.html#id129)].\n",
"\n",
"\n",
"\n",
" \n",
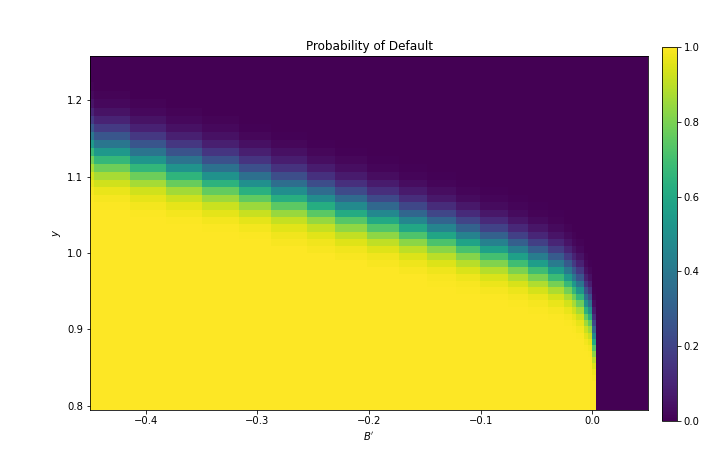
"We can use the results of the computation to study the default probability $ \\delta(B', y) $\n",
"defined in [(13.4)](#equation-delta).\n",
"\n",
"The next plot shows these default probabilities over $ (B', y) $ as a heat map.\n",
"\n",
"\n",
"\n",
" \n",
"As anticipated, the probability that the government chooses to default in the following period\n",
"increases with indebtedness and falls with income.\n",
"\n",
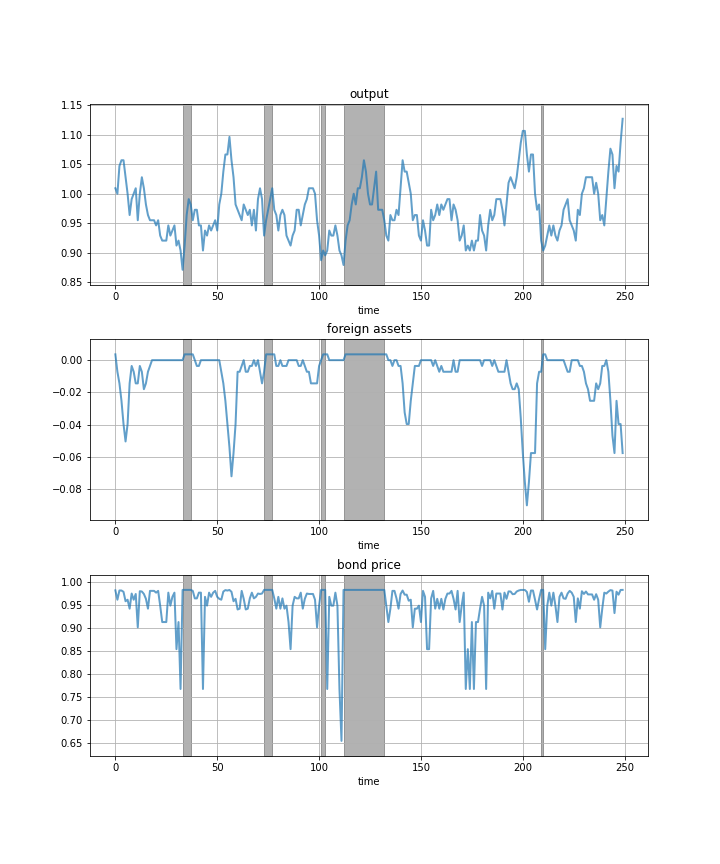
"Next let’s run a time series simulation of $ \\{y_t\\} $, $ \\{B_t\\} $ and $ q(B_{t+1}, y_t) $.\n",
"\n",
"The grey vertical bars correspond to periods when the economy is excluded from financial markets because of a past default.\n",
"\n",
"\n",
"\n",
" \n",
"One notable feature of the simulated data is the nonlinear response of interest rates.\n",
"\n",
"Periods of relative stability are followed by sharp spikes in the discount rate on government debt."
]
},
{
"cell_type": "markdown",
"id": "57e2c49d",
"metadata": {},
"source": [
"## Exercises\n",
"\n",
"\n",
"<a id='arellano-ex1'></a>"
]
},
{
"cell_type": "markdown",
"id": "88fcf1d6",
"metadata": {},
"source": [
"## Exercise 13.1\n",
"\n",
"To the extent that you can, replicate the figures shown above\n",
"\n",
"- Use the parameter values listed as defaults in `Arellano_Economy`. \n",
"- The time series will of course vary depending on the shock draws. "
]
},
{
"cell_type": "markdown",
"id": "873d3de6",
"metadata": {},
"source": [
"## Solution to[ Exercise 13.1](https://python-advanced.quantecon.org/#arella_ex1)\n",
"\n",
"Compute the value function, policy and equilibrium prices"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "67ebb3d2",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"ae = Arellano_Economy()"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "cf7a91a3",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"v_c, v_d, q, B_star = solve(ae)"
]
},
{
"cell_type": "markdown",
"id": "ff0a095d",
"metadata": {},
"source": [
"Compute the bond price schedule as seen in figure 3 of Arellano (2008)"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "f6d21f69",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"# Unpack some useful names\n",
"B_grid, y_grid, P = ae.B_grid, ae.y_grid, ae.P\n",
"B_grid_size, y_grid_size = len(B_grid), len(y_grid)\n",
"r = ae.r\n",
"\n",
"# Create \"Y High\" and \"Y Low\" values as 5% devs from mean\n",
"high, low = np.mean(y_grid) * 1.05, np.mean(y_grid) * .95\n",
"iy_high, iy_low = (np.searchsorted(y_grid, x) for x in (high, low))\n",
"\n",
"fig, ax = plt.subplots(figsize=(10, 6.5))\n",
"ax.set_title(\"Bond price schedule $q(y, B')$\")\n",
"\n",
"# Extract a suitable plot grid\n",
"x = []\n",
"q_low = []\n",
"q_high = []\n",
"for i, B in enumerate(B_grid):\n",
" if -0.35 <= B <= 0: # To match fig 3 of Arellano\n",
" x.append(B)\n",
" q_low.append(q[i, iy_low])\n",
" q_high.append(q[i, iy_high])\n",
"ax.plot(x, q_high, label=\"$y_H$\", lw=2, alpha=0.7)\n",
"ax.plot(x, q_low, label=\"$y_L$\", lw=2, alpha=0.7)\n",
"ax.set_xlabel(\"$B'$\")\n",
"ax.legend(loc='upper left', frameon=False)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "1363197f",
"metadata": {},
"source": [
"Draw a plot of the value functions"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "a22d4b0f",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"v = np.maximum(v_c, np.reshape(v_d, (1, y_grid_size)))\n",
"\n",
"fig, ax = plt.subplots(figsize=(10, 6.5))\n",
"ax.set_title(\"Value Functions\")\n",
"ax.plot(B_grid, v[:, iy_high], label=\"$y_H$\", lw=2, alpha=0.7)\n",
"ax.plot(B_grid, v[:, iy_low], label=\"$y_L$\", lw=2, alpha=0.7)\n",
"ax.legend(loc='upper left')\n",
"ax.set(xlabel=\"$B$\", ylabel=\"$v(y, B)$\")\n",
"ax.set_xlim(min(B_grid), max(B_grid))\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "a82f865f",
"metadata": {},
"source": [
"Draw a heat map for default probability"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "30f5e88c",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"xx, yy = B_grid, y_grid\n",
"zz = np.empty_like(v_c)\n",
"\n",
"for B_idx in range(B_grid_size):\n",
" for y_idx in range(y_grid_size):\n",
" zz[B_idx, y_idx] = P[y_idx, v_c[B_idx, :] < v_d].sum()\n",
"\n",
"# Create figure\n",
"fig, ax = plt.subplots(figsize=(10, 6.5))\n",
"hm = ax.pcolormesh(xx, yy, zz.T)\n",
"cax = fig.add_axes([.92, .1, .02, .8])\n",
"fig.colorbar(hm, cax=cax)\n",
"ax.axis([xx.min(), 0.05, yy.min(), yy.max()])\n",
"ax.set(xlabel=\"$B'$\", ylabel=\"$y$\", title=\"Probability of Default\")\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "16c0fb97",
"metadata": {},
"source": [
"Plot a time series of major variables simulated from the model"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "658ee5b4",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"T = 250\n",
"np.random.seed(42)\n",
"y_sim, y_a_sim, B_sim, q_sim, d_sim = simulate(ae, T, v_c, v_d, q, B_star)\n",
"\n",
"# Pick up default start and end dates\n",
"start_end_pairs = []\n",
"i = 0\n",
"while i < len(d_sim):\n",
" if d_sim[i] == 0:\n",
" i += 1\n",
" else:\n",
" # If we get to here we're in default\n",
" start_default = i\n",
" while i < len(d_sim) and d_sim[i] == 1:\n",
" i += 1\n",
" end_default = i - 1\n",
" start_end_pairs.append((start_default, end_default))\n",
"\n",
"plot_series = (y_sim, B_sim, q_sim)\n",
"titles = 'output', 'foreign assets', 'bond price'\n",
"\n",
"fig, axes = plt.subplots(len(plot_series), 1, figsize=(10, 12))\n",
"fig.subplots_adjust(hspace=0.3)\n",
"\n",
"for ax, series, title in zip(axes, plot_series, titles):\n",
" # Determine suitable y limits\n",
" s_max, s_min = max(series), min(series)\n",
" s_range = s_max - s_min\n",
" y_max = s_max + s_range * 0.1\n",
" y_min = s_min - s_range * 0.1\n",
" ax.set_ylim(y_min, y_max)\n",
" for pair in start_end_pairs:\n",
" ax.fill_between(pair, (y_min, y_min), (y_max, y_max),\n",
" color='k', alpha=0.3)\n",
" ax.grid()\n",
" ax.plot(range(T), series, lw=2, alpha=0.7)\n",
" ax.set(title=title, xlabel=\"time\")\n",
"\n",
"plt.show()"
]
}
],
"metadata": {
"date": 1754298583.3604662,
"filename": "arellano.md",
"kernelspec": {
"display_name": "Python",
"language": "python3",
"name": "python3"
},
"title": "Default Risk and Income Fluctuations"
},
"nbformat": 4,
"nbformat_minor": 5
}