45. Optimal Taxation with State-Contingent Debt#
In addition to what’s in Anaconda, this lecture will need the following libraries:
!pip install --upgrade quantecon
45.1. Overview#
This lecture describes a celebrated model of optimal fiscal policy by Robert E. Lucas, Jr., and Nancy Stokey [Lucas and Stokey, 1983].
The model revisits classic issues about how to pay for a war.
Here a war means a more or less temporary surge in an exogenous government expenditure process.
The model features
a government that must finance an exogenous stream of government expenditures with either
a flat rate tax on labor, or
purchases and sales from a full array of Arrow state-contingent securities
a representative household that values consumption and leisure
a linear production function mapping labor into a single good
a Ramsey planner who at time
After first presenting the model in a space of sequences, we shall represent it recursively in terms of two Bellman equations formulated along lines that we encountered in Dynamic Stackelberg models.
As in Dynamic Stackelberg models, to apply dynamic programming we shall define the state vector artfully.
In particular, we shall include forward-looking variables that summarize optimal responses of private agents to a Ramsey plan.
See Optimal taxation for analysis within a linear-quadratic setting.
Let’s start with some standard imports:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import root
from quantecon import MarkovChain
from quantecon.optimize.nelder_mead import nelder_mead
from numba import njit, prange, float64
from numba.experimental import jitclass
45.2. A Competitive Equilibrium with Distorting Taxes#
At time
For
We begin by assuming that government purchases
Let
A representative household is endowed with one unit of time that can be divided
between leisure
Output equals
A representative household’s preferences over
where the utility function
The technology pins down a pre-tax wage rate to unity for all
The government imposes a flat-rate tax
There are complete markets in one-period Arrow securities.
One unit of an Arrow security issued at time
The government issues one-period Arrow securities each period.
The government has a sequence of budget constraints whose time
where
Government debt
The representative household has a sequence of budget constraints whose time
A government policy is an exogenous sequence
A feasible allocation is a consumption-labor supply plan
A price system is a sequence of Arrow security prices
The household faces the price system as a price-taker and takes the government policy as given.
The household chooses
A competitive equilibrium with distorting taxes is a feasible allocation, a price system, and a government policy such that
Given the price system and the government policy, the allocation solves the household’s optimization problem.
Given the allocation, government policy, and price system, the government’s budget constraint is satisfied for all
Note
There are many competitive equilibria with distorting taxes.
They are indexed by different government policies.
The Ramsey problem or optimal taxation problem is to choose a competitive equilibrium with distorting taxes that maximizes (45.3).
45.2.1. Arrow-Debreu Version of Price System#
We find it convenient sometimes to work with the Arrow-Debreu price system that is implied by a sequence of Arrow securities prices.
Let
The following recursion relates Arrow-Debreu prices
Arrow-Debreu prices are useful when we want to compress a sequence of budget constraints into a single intertemporal budget constraint, as we shall find it convenient to do below.
45.2.2. Primal Approach#
We apply a popular approach to solving a Ramsey problem, called the primal approach.
The idea is to use first-order conditions for household optimization to eliminate taxes and prices in favor of quantities, then pose an optimization problem cast entirely in terms of quantities.
After Ramsey quantities have been found, taxes and prices can then be unwound from the allocation.
The primal approach uses four steps:
Obtain first-order conditions of the household’s problem and solve them for
Substitute these expressions for taxes and prices in terms of the allocation into the household’s present-value budget constraint.
This intertemporal constraint involves only the allocation and is regarded as an implementability constraint.
Find the allocation that maximizes the utility of the representative household (45.3) subject to the feasibility constraints (45.1) and (45.2) and the implementability condition derived in step 2.
This optimal allocation is called the Ramsey allocation.
Use the Ramsey allocation together with the formulas from step 1 to find taxes and prices.
45.2.3. The Implementability Constraint#
By sequential substitution of one one-period budget constraint (45.5) into another, we can obtain the household’s present-value budget constraint:
To approach the Ramsey problem, we study the household’s optimization problem.
First-order conditions for the household’s problem for
and
where
Equation (45.9) implies that the Arrow-Debreu price system satisfies
(The stochastic process
Using the first-order conditions (45.8) and (45.9) to eliminate taxes and prices from (45.7), we derive the implementability condition
The Ramsey problem is to choose a feasible allocation that maximizes
subject to (45.11).
45.2.4. Solution Details#
First, define a “pseudo utility function”
where
Next form the Lagrangian
where
Given an initial government debt
The first-order conditions for the Ramsey problem for periods
and
Please note how these first-order conditions differ between
It is instructive to use first-order conditions (45.15) for
For convenience, we suppress the time subscript and the index
where we have imposed conditions (45.1) and (45.2).
Equation (45.17) is one equation that can be solved to express the
unknown
We also know that time
Notice that a counterpart to
But things are different for time
An analogous argument for the
These outcomes mean that the following statement would be true even when
government purchases are history-dependent functions
Proposition:
If government purchases are equal after two histories
then it follows from (45.17) that the Ramsey choices of consumption and leisure,
The proposition asserts that the optimal allocation is a function of the
currently realized quantity of government purchases
45.2.5. The Ramsey Allocation for a Given Multiplier#
Temporarily take
We shall compute
Evidently, for
But for
Thus, while
The absence of
Of course,
45.2.6. Further Specialization#
At this point, it is useful to specialize the model in the following ways.
We assume that
Also, assume that government purchases
We maintain these assumptions throughout the remainder of this lecture.
45.2.7. Determining the Lagrange Multiplier#
We complete the Ramsey plan by computing the Lagrange multiplier
Government budget balance restricts
The household’s first-order conditions imply
and the implied one-period Arrow securities prices
Substituting from (45.19), (45.20), and the feasibility condition (45.2) into the recursive version (45.5) of the household budget constraint gives
Define
Notice that
Hence the equation shares much of the structure of a simple asset pricing equation with
We learned earlier that for a Ramsey allocation
That means that we can express equation (45.21) as
where
Given
If we let
This is a system of
In these equations, by
After solving for
where division here means an element-by-element division of the respective
components of the
Here is a computational algorithm:
Start with a guess for the value for
these are
Solve the
these depend on
Find a
by gradually raising
After computing a Ramsey allocation, recover the flat tax rate on labor from (45.8) and the implied one-period Arrow securities prices from (45.9).
In summary, when
45.2.8. Time Inconsistency#
Let
Then
A time
A time
The means that a Ramsey plan is not time consistent.
Another way to say the same thing is that a Ramsey plan is time inconsistent.
The reason is that a continuation Ramsey plan takes
We shall discuss this more below.
45.2.9. Specification with CRRA Utility#
In our calculations below and in a subsequent lecture based on an extension of the Lucas-Stokey model by Aiyagari, Marcet, Sargent, and Seppälä (2002) [Aiyagari et al., 2002], we shall modify the one-period utility function assumed above.
(We adopted the preceding utility specification because it was the one used in the original Lucas-Stokey paper [Lucas and Stokey, 1983]. We shall soon revert to that specification in a subsequent section.)
We will modify their specification by instead assuming that the representative agent has utility function
where
We continue to assume that
We eliminate leisure from the model.
We also eliminate Lucas and Stokey’s restriction that
We replace these two things with the assumption that
labor
With these adjustments, the analysis of Lucas and Stokey prevails once we make the following replacements
With these understandings, equations (45.17) and (45.18) simplify in the case of the CRRA utility function.
They become
and
In equation (45.27), it is understood that
In addition, the time
where
In equation (45.29), it is understood that
45.2.10. Sequence Implementation#
The above steps are implemented in a class called SequentialLS
class SequentialLS:
'''
Class that takes a preference object, state transition matrix,
and state contingent government expenditure plan as inputs, and
solves the sequential allocation problem described above.
It returns optimal allocations about consumption and labor supply,
as well as the multiplier on the implementability constraint Φ.
'''
def __init__(self,
pref,
π=np.full((2, 2), 0.5),
g=np.array([0.1, 0.2])):
# Initialize from pref object attributes
self.β, self.π, self.g = pref.β, π, g
self.mc = MarkovChain(self.π)
self.S = len(π) # Number of states
self.pref = pref
# Find the first best allocation
self.find_first_best()
def FOC_first_best(self, c, g):
'''
First order conditions that characterize
the first best allocation.
'''
pref = self.pref
Uc, Ul = pref.Uc, pref.Ul
n = c + g
l = 1 - n
return Uc(c, l) - Ul(c, l)
def find_first_best(self):
'''
Find the first best allocation
'''
S, g = self.S, self.g
res = root(self.FOC_first_best, np.full(S, 0.5), args=(g,))
if (res.fun > 1e-10).any():
raise Exception('Could not find first best')
self.cFB = res.x
self.nFB = self.cFB + g
def FOC_time1(self, c, Φ, g):
'''
First order conditions that characterize
optimal time 1 allocation problems.
'''
pref = self.pref
Uc, Ucc, Ul, Ull, Ulc = pref.Uc, pref.Ucc, pref.Ul, pref.Ull, pref.Ulc
n = c + g
l = 1 - n
LHS = (1 + Φ) * Uc(c, l) + Φ * (c * Ucc(c, l) - n * Ulc(c, l))
RHS = (1 + Φ) * Ul(c, l) + Φ * (c * Ulc(c, l) - n * Ull(c, l))
diff = LHS - RHS
return diff
def time1_allocation(self, Φ):
'''
Computes optimal allocation for time t >= 1 for a given Φ
'''
pref = self.pref
S, g = self.S, self.g
# use the first best allocation as intial guess
res = root(self.FOC_time1, self.cFB, args=(Φ, g))
if (res.fun > 1e-10).any():
raise Exception('Could not find LS allocation.')
c = res.x
n = c + g
l = 1 - n
# Compute x
I = pref.Uc(c, n) * c - pref.Ul(c, l) * n
x = np.linalg.solve(np.eye(S) - self.β * self.π, I)
return c, n, x
def FOC_time0(self, c0, Φ, g0, b0):
'''
First order conditions that characterize
time 0 allocation problem.
'''
pref = self.pref
Ucc, Ulc = pref.Ucc, pref.Ulc
n0 = c0 + g0
l0 = 1 - n0
diff = self.FOC_time1(c0, Φ, g0)
diff -= Φ * (Ucc(c0, l0) - Ulc(c0, l0)) * b0
return diff
def implementability(self, Φ, b0, s0, cn0_arr):
'''
Compute the differences between the RHS and LHS
of the implementability constraint given Φ,
initial debt, and initial state.
'''
pref, π, g, β = self.pref, self.π, self.g, self.β
Uc, Ul = pref.Uc, pref.Ul
g0 = self.g[s0]
c, n, x = self.time1_allocation(Φ)
res = root(self.FOC_time0, cn0_arr[0], args=(Φ, g0, b0))
c0 = res.x
n0 = c0 + g0
l0 = 1 - n0
cn0_arr[:] = c0.item(), n0.item()
LHS = Uc(c0, l0) * b0
RHS = Uc(c0, l0) * c0 - Ul(c0, l0) * n0 + β * π[s0] @ x
return RHS - LHS
def time0_allocation(self, b0, s0):
'''
Finds the optimal time 0 allocation given
initial government debt b0 and state s0
'''
# use the first best allocation as initial guess
cn0_arr = np.array([self.cFB[s0], self.nFB[s0]])
res = root(self.implementability, 0., args=(b0, s0, cn0_arr))
if (res.fun > 1e-10).any():
raise Exception('Could not find time 0 LS allocation.')
Φ = res.x[0]
c0, n0 = cn0_arr
return Φ, c0, n0
def τ(self, c, n):
'''
Computes τ given c, n
'''
pref = self.pref
Uc, Ul = pref.Uc, pref.Ul
return 1 - Ul(c, 1-n) / Uc(c, 1-n)
def simulate(self, b0, s0, T, sHist=None):
'''
Simulates planners policies for T periods
'''
pref, π, β = self.pref, self.π, self.β
Uc = pref.Uc
if sHist is None:
sHist = self.mc.simulate(T, s0)
cHist, nHist, Bhist, τHist, ΦHist = np.empty((5, T))
RHist = np.empty(T-1)
# Time 0
Φ, cHist[0], nHist[0] = self.time0_allocation(b0, s0)
τHist[0] = self.τ(cHist[0], nHist[0])
Bhist[0] = b0
ΦHist[0] = Φ
# Time 1 onward
for t in range(1, T):
c, n, x = self.time1_allocation(Φ)
τ = self.τ(c, n)
u_c = Uc(c, 1-n)
s = sHist[t]
Eu_c = π[sHist[t-1]] @ u_c
cHist[t], nHist[t], Bhist[t], τHist[t] = c[s], n[s], x[s] / u_c[s], τ[s]
RHist[t-1] = Uc(cHist[t-1], 1-nHist[t-1]) / (β * Eu_c)
ΦHist[t] = Φ
gHist = self.g[sHist]
yHist = nHist
return [cHist, nHist, Bhist, τHist, gHist, yHist, sHist, ΦHist, RHist]
45.3. Recursive Formulation of the Ramsey Problem#
We now temporarily revert to Lucas and Stokey’s specification.
We start by noting that
But backward-looking.
45.3.1. Intertemporal Delegation#
To express a Ramsey plan recursively, we imagine that a time
A “continuation Ramsey planner” at time
A key step in representing a Ramsey plan recursively is
to regard the marginal utility scaled government debts
Continuation Ramsey planners do this by choosing continuation policies that induce the representative
household to make choices that imply that
A time
A time
While a time
Furthermore, the Ramsey planner cares about
The time
These lines of delegated authorities and
responsibilities across time express the continuation Ramsey planners’
obligations to implement their parts of an original Ramsey plan that had been
designed once-and-for-all at time
45.3.2. Two Bellman Equations#
After
Let
Let
We work backward by preparing a Bellman equation for
45.3.3. The Continuation Ramsey Problem#
The Bellman equation for a time
where maximization over
Here
For each given value of
Associated with a value function
45.3.4. The Ramsey Problem#
The Bellman equation of the time
where maximization over
coming from restriction (45.26).
Associated with a value function
Notice the appearance of state variables
The value function
45.3.5. First-Order Conditions#
Attach a Lagrange multiplier
Time
for
for
Given
Equation (45.36) implies
Time
for
Notice similarities and differences between the first-order
conditions for
An additional term is present in (45.40) except in three special cases
initial government assets are sufficiently large to finance all government purchases with interest earnings from those assets so that
Except in these special cases, the allocation and the labor tax rate as
functions of
Naturally, the first-order conditions in this recursive formulation of the Ramsey problem agree with the first-order conditions derived when we first formulated the Ramsey plan in the space of sequences.
45.3.6. State Variable Degeneracy#
Equations (45.38) and (45.39) imply that
for all
When
Given
45.3.7. Manifestations of Time Inconsistency#
While the marginal utility adjusted level of government debt
The time
The discrepancy in state variables faced by the time
The time
The time
In contrast, time
When government expenditures
This means that
This in turn means that prices of
one-period Arrow securities
The differences between these
time
45.3.8. Recursive Implementation#
The above steps are implemented in a class called RecursiveLS.
class RecursiveLS:
'''
Compute the planner's allocation by solving Bellman
equation.
'''
def __init__(self,
pref,
x_grid,
π=np.full((2, 2), 0.5),
g=np.array([0.1, 0.2])):
self.π, self.g, self.S = π, g, len(π)
self.pref, self.x_grid = pref, x_grid
bounds = np.empty((self.S, 2))
# bound for n
bounds[0] = 0, 1
# bound for xprime
for s in range(self.S-1):
bounds[s+1] = x_grid.min(), x_grid.max()
self.bounds = bounds
# initialization of time 1 value function
self.V = None
def time1_allocation(self, V=None, tol=1e-7):
'''
Solve the optimal time 1 allocation problem
by iterating Bellman value function.
'''
π, g, S = self.π, self.g, self.S
pref, x_grid, bounds = self.pref, self.x_grid, self.bounds
# initial guess of value function
if V is None:
V = np.zeros((len(x_grid), S))
# initial guess of policy
z = np.empty((len(x_grid), S, S+2))
# guess of n
z[:, :, 1] = 0.5
# guess of xprime
for s in range(S):
for i in range(S-1):
z[:, s, i+2] = x_grid
while True:
# value function iteration
V_new, z_new = T(V, z, pref, π, g, x_grid, bounds)
if np.max(np.abs(V - V_new)) < tol:
break
V = V_new
z = z_new
self.V = V_new
self.z1 = z_new
self.c1 = z_new[:, :, 0]
self.n1 = z_new[:, :, 1]
self.xprime1 = z_new[:, :, 2:]
return V_new, z_new
def time0_allocation(self, b0, s0):
'''
Find the optimal time 0 allocation by maximization.
'''
if self.V is None:
self.time1_allocation()
π, g, S = self.π, self.g, self.S
pref, x_grid, bounds = self.pref, self.x_grid, self.bounds
V, z1 = self.V, self.z1
x = 1. # x is arbitrary
res = nelder_mead(obj_V,
z1[0, s0, 1:-1],
args=(x, s0, V, pref, π, g, x_grid, b0),
bounds=bounds,
tol_f=1e-10)
n0, xprime0 = IC(res.x, x, s0, b0, pref, π, g)
c0 = n0 - g[s0]
z0 = np.array([c0, n0, *xprime0])
self.z0 = z0
self.n0 = n0
self.c0 = n0 - g[s0]
self.xprime0 = xprime0
return z0
def τ(self, c, n):
'''
Computes τ given c, n
'''
pref = self.pref
uc, ul = pref.Uc(c, 1-n), pref.Ul(c, 1-n)
return 1 - ul / uc
def simulate(self, b0, s0, T, sHist=None):
'''
Simulates Ramsey plan for T periods
'''
pref, π = self.pref, self.π
Uc = pref.Uc
if sHist is None:
sHist = self.mc.simulate(T, s0)
cHist, nHist, Bhist, τHist, xHist = np.empty((5, T))
RHist = np.zeros(T-1)
# Time 0
self.time0_allocation(b0, s0)
cHist[0], nHist[0], xHist[0] = self.c0, self.n0, self.xprime0[s0]
τHist[0] = self.τ(cHist[0], nHist[0])
Bhist[0] = b0
# Time 1 onward
for t in range(1, T):
s, x = sHist[t], xHist[t-1]
cHist[t] = np.interp(x, self.x_grid, self.c1[:, s])
nHist[t] = np.interp(x, self.x_grid, self.n1[:, s])
τHist[t] = self.τ(cHist[t], nHist[t])
Bhist[t] = x / Uc(cHist[t], 1-nHist[t])
c, n = np.empty((2, self.S))
for sprime in range(self.S):
c[sprime] = np.interp(x, x_grid, self.c1[:, sprime])
n[sprime] = np.interp(x, x_grid, self.n1[:, sprime])
Euc = π[sHist[t-1]] @ Uc(c, 1-n)
RHist[t-1] = Uc(cHist[t-1], 1-nHist[t-1]) / (self.pref.β * Euc)
gHist = self.g[sHist]
yHist = nHist
if t < T-1:
sprime = sHist[t+1]
xHist[t] = np.interp(x, self.x_grid, self.xprime1[:, s, sprime])
return [cHist, nHist, Bhist, τHist, gHist, yHist, xHist, RHist]
# Helper functions
@njit(parallel=True)
def T(V, z, pref, π, g, x_grid, bounds):
'''
One step iteration of Bellman value function.
'''
S = len(π)
V_new = np.empty_like(V)
z_new = np.empty_like(z)
for i in prange(len(x_grid)):
x = x_grid[i]
for s in prange(S):
res = nelder_mead(obj_V,
z[i, s, 1:-1],
args=(x, s, V, pref, π, g, x_grid),
bounds=bounds,
tol_f=1e-10)
# optimal policy
n, xprime = IC(res.x, x, s, None, pref, π, g)
z_new[i, s, 0] = n - g[s] # c
z_new[i, s, 1] = n # n
z_new[i, s, 2:] = xprime # xprime
V_new[i, s] = res.fun
return V_new, z_new
@njit
def obj_V(z_sub, x, s, V, pref, π, g, x_grid, b0=None):
'''
The objective on the right hand side of the Bellman equation.
z_sub contains guesses of n and xprime[:-1].
'''
S = len(π)
β, U = pref.β, pref.U
# find (n, xprime) that satisfies implementability constraint
n, xprime = IC(z_sub, x, s, b0, pref, π, g)
c, l = n-g[s], 1-n
# if xprime[-1] violates bound, return large penalty
if (xprime[-1] < x_grid.min()):
return -1e9 * (1 + np.abs(xprime[-1] - x_grid.min()))
elif (xprime[-1] > x_grid.max()):
return -1e9 * (1 + np.abs(xprime[-1] - x_grid.max()))
# prepare Vprime vector
Vprime = np.empty(S)
for sprime in range(S):
Vprime[sprime] = np.interp(xprime[sprime], x_grid, V[:, sprime])
# compute the objective value
obj = U(c, l) + β * π[s] @ Vprime
return obj
@njit
def IC(z_sub, x, s, b0, pref, π, g):
'''
Find xprime[-1] that satisfies the implementability condition
given the guesses of n and xprime[:-1].
'''
β, Uc, Ul = pref.β, pref.Uc, pref.Ul
n = z_sub[0]
xprime = np.empty(len(π))
xprime[:-1] = z_sub[1:]
c, l = n-g[s], 1-n
uc = Uc(c, l)
ul = Ul(c, l)
if b0 is None:
diff = x
else:
diff = uc * b0
diff -= uc * (n - g[s]) - ul * n + β * π[s][:-1] @ xprime[:-1]
xprime[-1] = diff / (β * π[s][-1])
return n, xprime
45.4. Examples#
We return to the setup with CRRA preferences described above.
45.4.1. Anticipated One-Period War#
This example illustrates in a simple setting how a Ramsey planner manages risk.
Government expenditures are known for sure in all periods except one
For
At
If there is war,
If there is no war
We define the components of the state vector as the following six
We think of these 6 states as corresponding to
The transition matrix is
Government expenditures at each state are
We assume that the representative agent has utility function
and set
Note
For convenience in terms of matching our code, we have expressed
utility as a function of
This utility function is implemented in the class CRRAutility.
crra_util_data = [
('β', float64),
('σ', float64),
('γ', float64)
]
@jitclass(crra_util_data)
class CRRAutility:
def __init__(self,
β=0.9,
σ=2,
γ=2):
self.β, self.σ, self.γ = β, σ, γ
# Utility function
def U(self, c, l):
# Note: `l` should not be interpreted as labor, it is an auxiliary
# variable used to conveniently match the code and the equations
# in the lecture
σ = self.σ
if σ == 1.:
U = np.log(c)
else:
U = (c**(1 - σ) - 1) / (1 - σ)
return U - (1-l) ** (1 + self.γ) / (1 + self.γ)
# Derivatives of utility function
def Uc(self, c, l):
return c ** (-self.σ)
def Ucc(self, c, l):
return -self.σ * c ** (-self.σ - 1)
def Ul(self, c, l):
return (1-l) ** self.γ
def Ull(self, c, l):
return -self.γ * (1-l) ** (self.γ - 1)
def Ucl(self, c, l):
return 0
def Ulc(self, c, l):
return 0
We set initial government debt
We can now plot the Ramsey tax under both realizations of time
black when
red when
π = np.array([[0, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, 0.5, 0.5, 0],
[0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 1]])
g = np.array([0.1, 0.1, 0.1, 0.2, 0.1, 0.1])
crra_pref = CRRAutility()
# Solve sequential problem
seq = SequentialLS(crra_pref, π=π, g=g)
sHist_h = np.array([0, 1, 2, 3, 5, 5, 5])
sHist_l = np.array([0, 1, 2, 4, 5, 5, 5])
sim_seq_h = seq.simulate(1, 0, 7, sHist_h)
sim_seq_l = seq.simulate(1, 0, 7, sHist_l)
fig, axes = plt.subplots(3, 2, figsize=(14, 10))
titles = ['Consumption', 'Labor Supply', 'Government Debt',
'Tax Rate', 'Government Spending', 'Output']
for ax, title, sim_l, sim_h in zip(axes.flatten(),
titles,
sim_seq_l[:6],
sim_seq_h[:6]):
ax.set(title=title)
ax.plot(sim_l, '-ok', sim_h, '-or', alpha=0.7)
ax.grid()
plt.tight_layout()
plt.show()
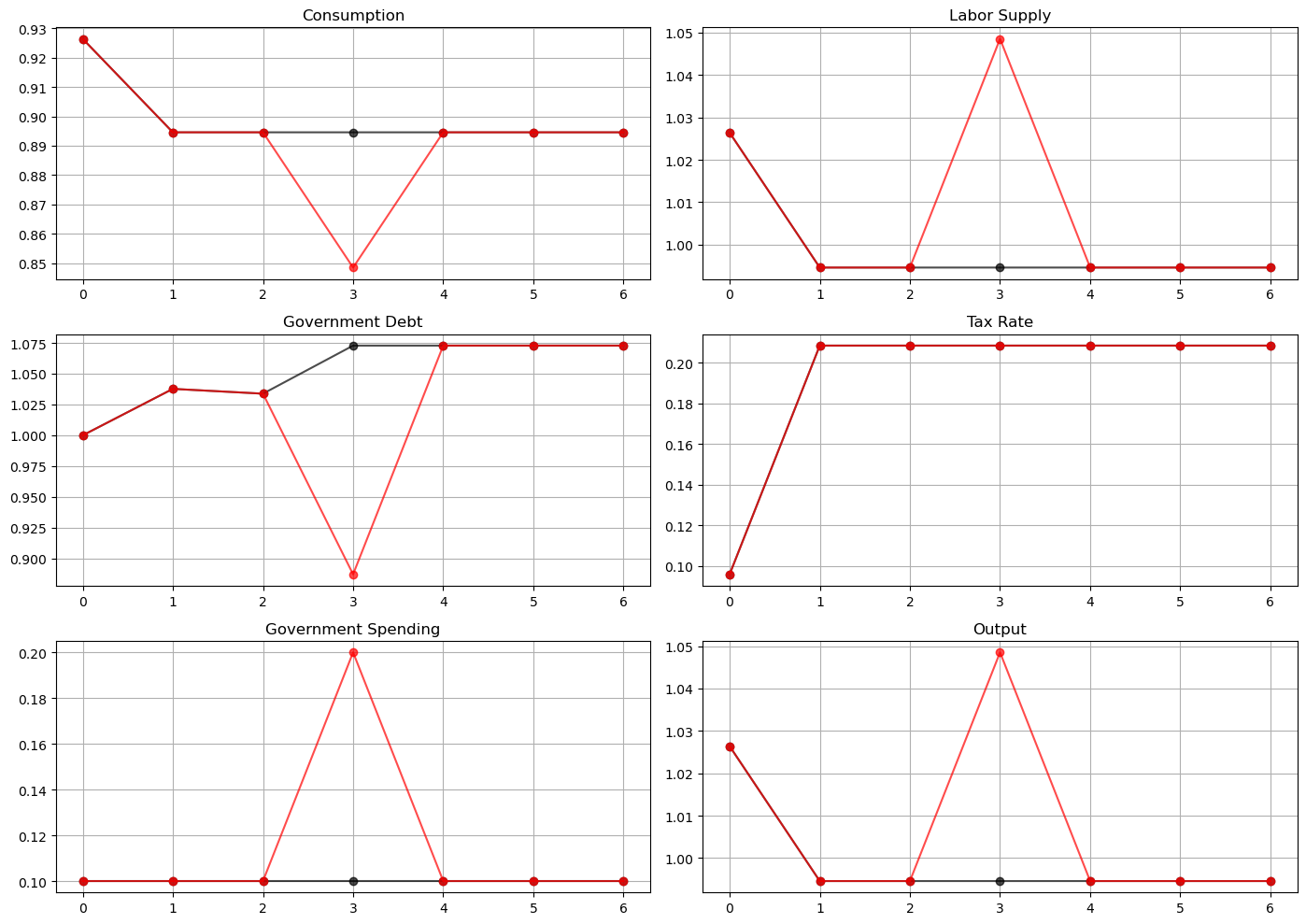
Tax smoothing
the tax rate is constant for all
For
For
Under other one-period utility functions, the time
the tax rate is the same at
We have assumed that at
It sets the time
It does this by increasing consumption at time
This has the consequence of lowering the time
A tax policy that makes time
Lowering the time
We see this in a figure below that plots the time path for the risk-free interest
rate under both realizations of the time
The following plot illustrates how the government lowers the interest rate at time 0 by raising consumption
fix, ax = plt.subplots(figsize=(8, 5))
ax.set_title('Gross Interest Rate')
ax.plot(sim_seq_l[-1], '-ok', sim_seq_h[-1], '-or', alpha=0.7)
ax.grid()
plt.show()
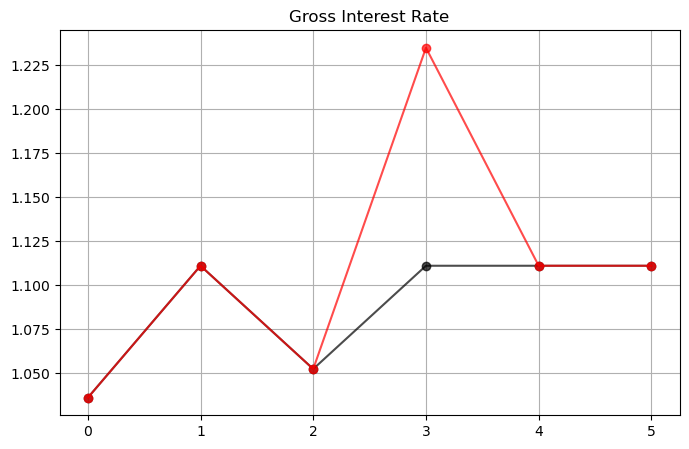
45.4.2. Government Saving#
At time
This is a consequence of it setting a lower tax rate at
At time
Its motive for doing this is that it anticipates a likely war at
At time
It purchases a security that pays off when
It sells a security that pays off when
These purchases are designed in such a way that regardless of whether or not there is a war at
The time
At times
45.4.3. Time 0 Manipulation of Interest Rate#
We have seen that when
By lowering this interest rate, the plan makes time
By doing this, it lowers the value of time
45.4.4. Time 0 and Time-Inconsistency#
In the preceding example, the Ramsey tax rate at time 0 differs from its value at time 1.
To explore what is going on here, let’s simplify things by removing the possibility of war at time
The Ramsey problem then includes no randomness because
The figure below plots the Ramsey tax rates and gross interest rates at time
tax_seq = SequentialLS(CRRAutility(), g=np.array([0.15]), π=np.ones((1, 1)))
n = 100
tax_policy = np.empty((n, 2))
interest_rate = np.empty((n, 2))
gov_debt = np.linspace(-1.5, 1, n)
for i in range(n):
tax_policy[i] = tax_seq.simulate(gov_debt[i], 0, 2)[3]
interest_rate[i] = tax_seq.simulate(gov_debt[i], 0, 3)[-1]
fig, axes = plt.subplots(2, 1, figsize=(10,8), sharex=True)
titles = ['Tax Rate', 'Gross Interest Rate']
for ax, title, plot in zip(axes, titles, [tax_policy, interest_rate]):
ax.plot(gov_debt, plot[:, 0], gov_debt, plot[:, 1], lw=2)
ax.set(title=title, xlim=(min(gov_debt), max(gov_debt)))
ax.grid()
axes[0].legend(('Time $t=0$', r'Time $t \geq 1$'))
axes[1].set_xlabel('Initial Government Debt')
fig.tight_layout()
plt.show()
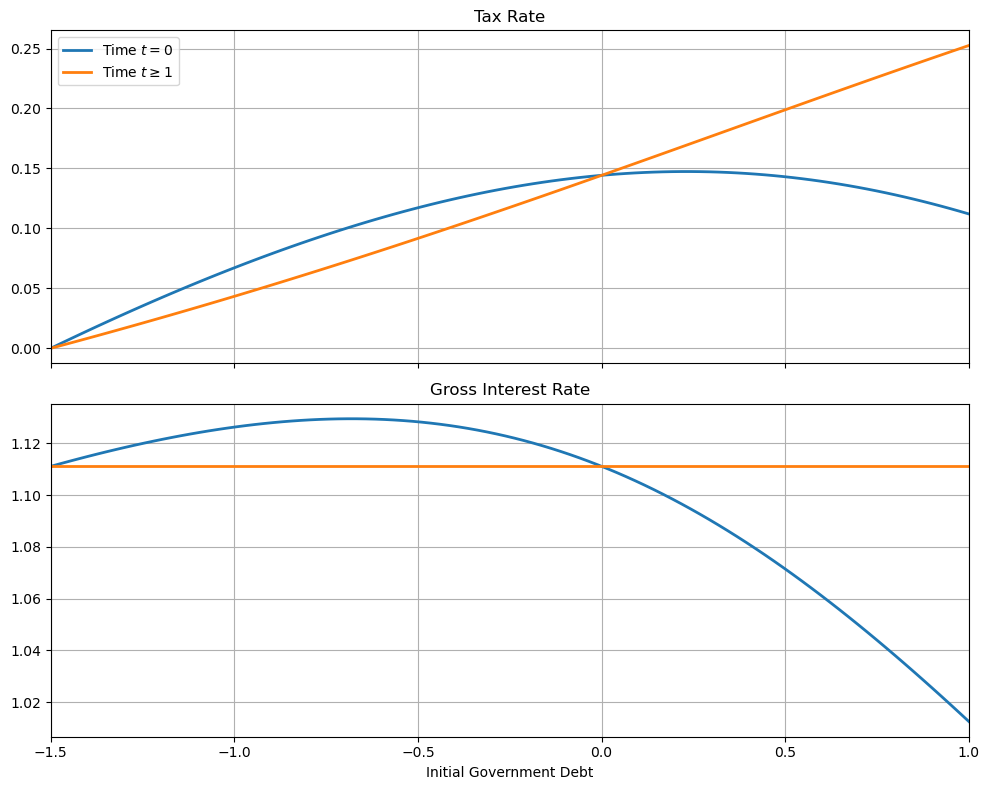
The figure indicates that if the government enters with positive debt, it sets
a tax rate at
By setting a lower tax rate at
It does this by increasing
Conversely, if
A side effect of lowering time
There are only two values of initial government debt at which the tax rate is
constant for all
The first is
Here the government can’t use the
The second occurs when the government enters with sufficiently large assets
that the Ramsey planner can achieve first best and sets
It is only for these two values of initial government debt that the Ramsey plan is time-consistent.
Another way of saying this is that, except for these two values of initial government debt, a continuation of a Ramsey plan is not a Ramsey plan.
To illustrate this, consider a Ramsey planner who starts with an initial
government debt
Call
The figure below shows both the tax rate at time 1 chosen by our original
Ramsey planner and what a new Ramsey planner would choose for its
time
tax_seq = SequentialLS(CRRAutility(), g=np.array([0.15]), π=np.ones((1, 1)))
n = 100
tax_policy = np.empty((n, 2))
τ_reset = np.empty((n, 2))
gov_debt = np.linspace(-1.5, 1, n)
for i in range(n):
tax_policy[i] = tax_seq.simulate(gov_debt[i], 0, 2)[3]
τ_reset[i] = tax_seq.simulate(gov_debt[i], 0, 1)[3]
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(gov_debt, tax_policy[:, 1], gov_debt, τ_reset, lw=2)
ax.set(xlabel='Initial Government Debt', title='Tax Rate',
xlim=(min(gov_debt), max(gov_debt)))
ax.legend((r'$\tau_1$', r'$\tau_1^R$'))
ax.grid()
fig.tight_layout()
plt.show()
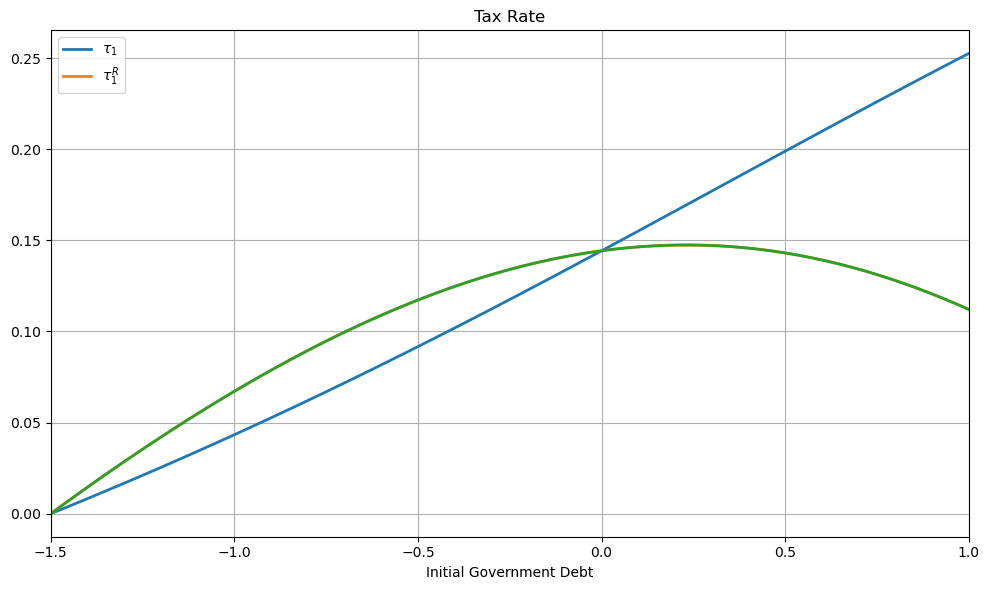
The tax rates in the figure are equal for only two values of initial government debt.
45.4.5. Tax Smoothing and non-CRRA Preferences#
The complete tax smoothing for
To see what is driving this outcome, we begin by noting that the Ramsey tax rate for
For CRRA preferences, we can exploit the relations
from the first-order conditions.
This equation immediately implies that the tax rate is constant.
For other preferences, the tax rate may not be constant.
For example, let the period utility function be
We will create a new class LogUtility to represent this utility function
log_util_data = [
('β', float64),
('ψ', float64)
]
@jitclass(log_util_data)
class LogUtility:
def __init__(self,
β=0.9,
ψ=0.69):
self.β, self.ψ = β, ψ
# Utility function
def U(self, c, l):
return np.log(c) + self.ψ * np.log(l)
# Derivatives of utility function
def Uc(self, c, l):
return 1 / c
def Ucc(self, c, l):
return -c**(-2)
def Ul(self, c, l):
return self.ψ / l
def Ull(self, c, l):
return -self.ψ / l**2
def Ucl(self, c, l):
return 0
def Ulc(self, c, l):
return 0
Also, suppose that
To compute the tax rate, we will use both the sequential and recursive approaches described above.
The figure below plots a sample path of the Ramsey tax rate
log_example = LogUtility()
# Solve sequential problem
seq_log = SequentialLS(log_example)
# Initialize grid for value function iteration and solve
x_grid = np.linspace(-3., 3., 200)
# Solve recursive problem
rec_log = RecursiveLS(log_example, x_grid)
T_length = 20
sHist = np.array([0, 0, 0, 0, 0,
0, 0, 0, 1, 1,
0, 0, 0, 1, 1,
1, 1, 1, 1, 0])
# Simulate
sim_seq = seq_log.simulate(0.5, 0, T_length, sHist)
sim_rec = rec_log.simulate(0.5, 0, T_length, sHist)
fig, axes = plt.subplots(3, 2, figsize=(14, 10))
titles = ['Consumption', 'Labor Supply', 'Government Debt',
'Tax Rate', 'Government Spending', 'Output']
for ax, title, sim_s, sim_b in zip(axes.flatten(), titles, sim_seq[:6], sim_rec[:6]):
ax.plot(sim_s, '-ob', sim_b, '-xk', alpha=0.7)
ax.set(title=title)
ax.grid()
axes.flatten()[0].legend(('Sequential', 'Recursive'))
fig.tight_layout()
plt.show()
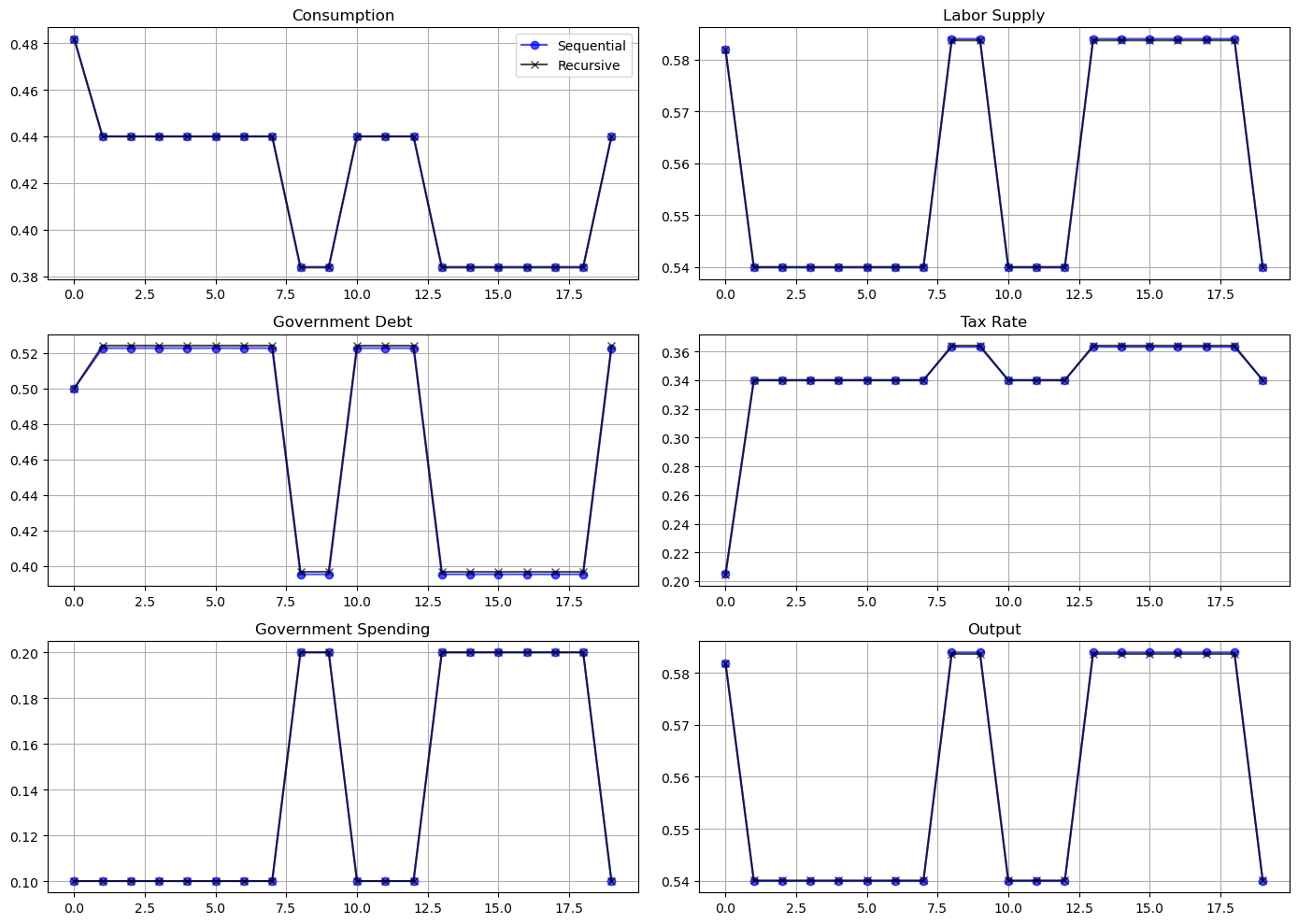
As should be expected, the recursive and sequential solutions produce almost identical allocations.
Unlike outcomes with CRRA preferences, the tax rate is not perfectly smoothed.
Instead, the government raises the tax rate when
45.4.6. Further Comments#
A related lecture describes an extension of the Lucas-Stokey model by Aiyagari, Marcet, Sargent, and Seppälä (2002) [Aiyagari et al., 2002].
In the AMSS economy, only a risk-free bond is traded.
That lecture compares the recursive representation of the Lucas-Stokey model presented in this lecture with one for an AMSS economy.
By comparing these recursive formulations, we shall glean a sense in which the dimension of the state is lower in the Lucas Stokey model.
Accompanying that difference in dimension will be different dynamics of government debt.
